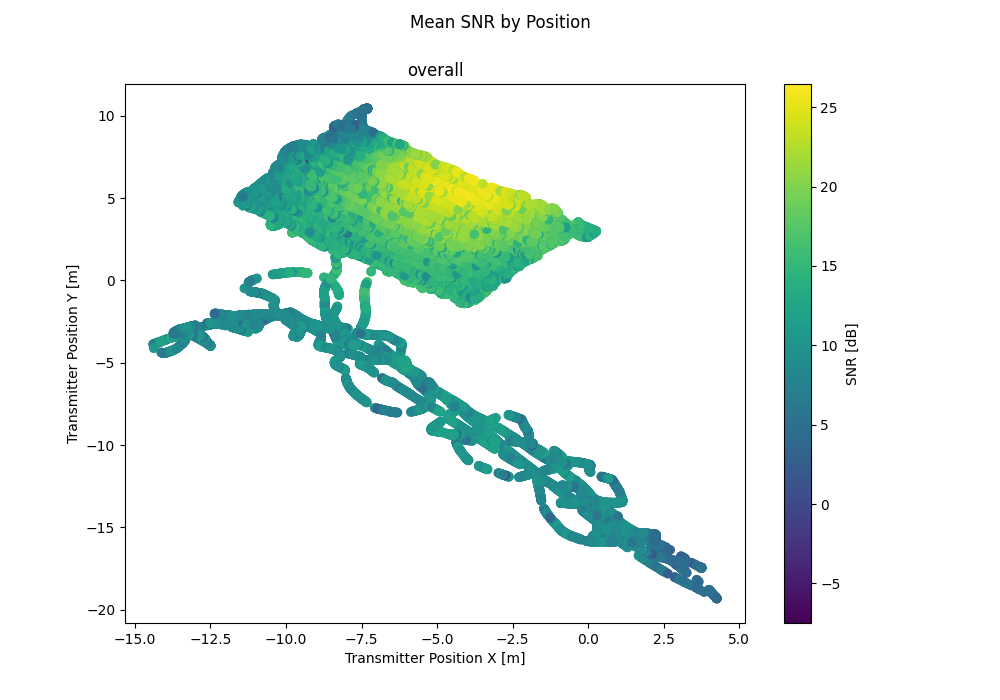
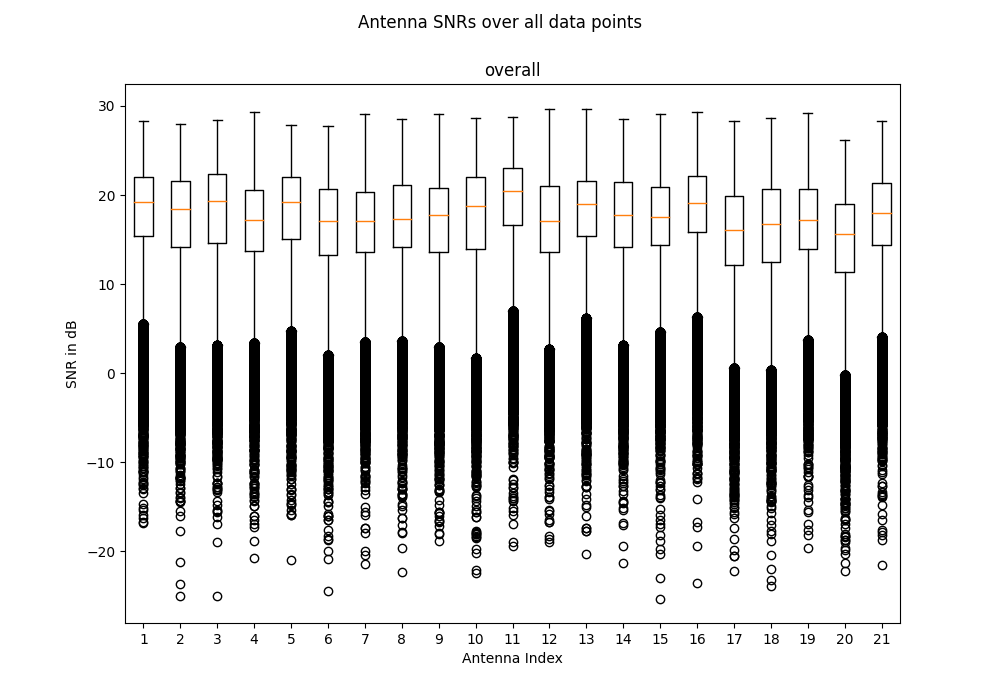
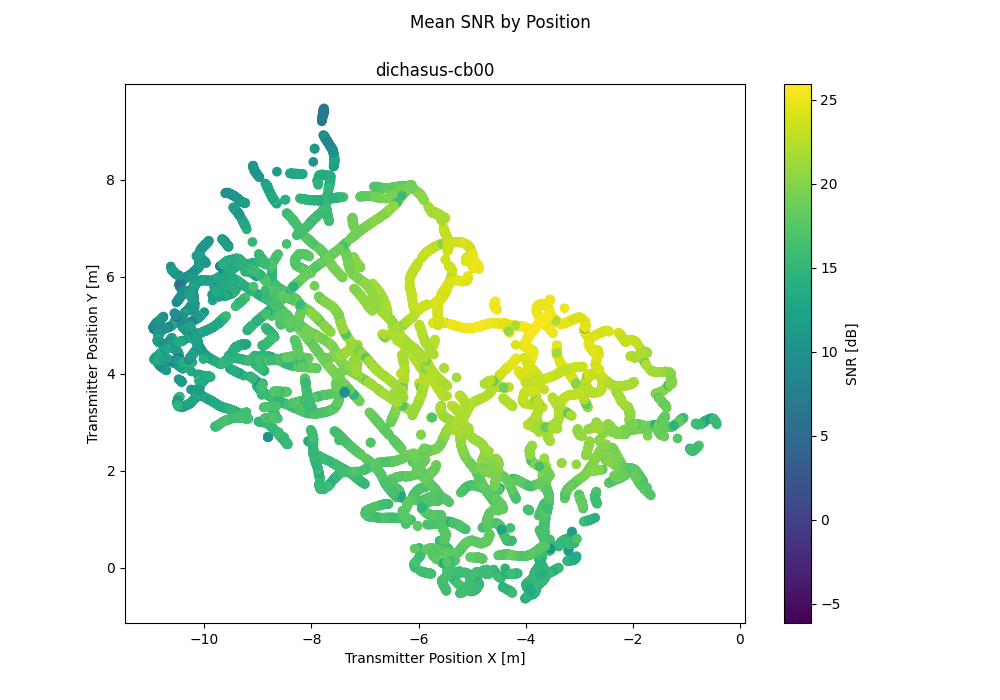
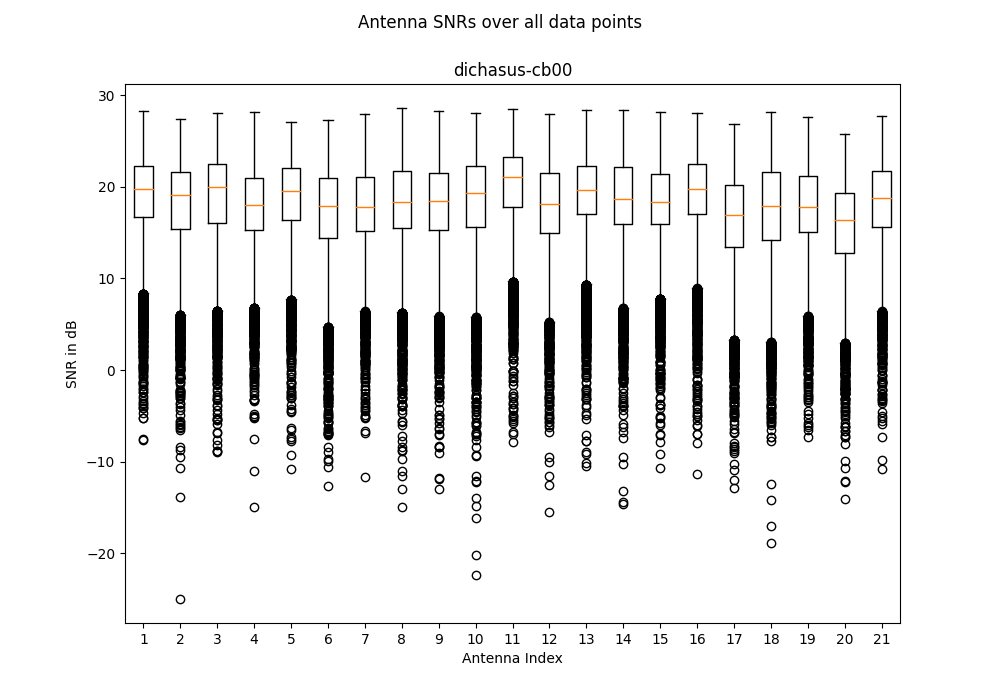
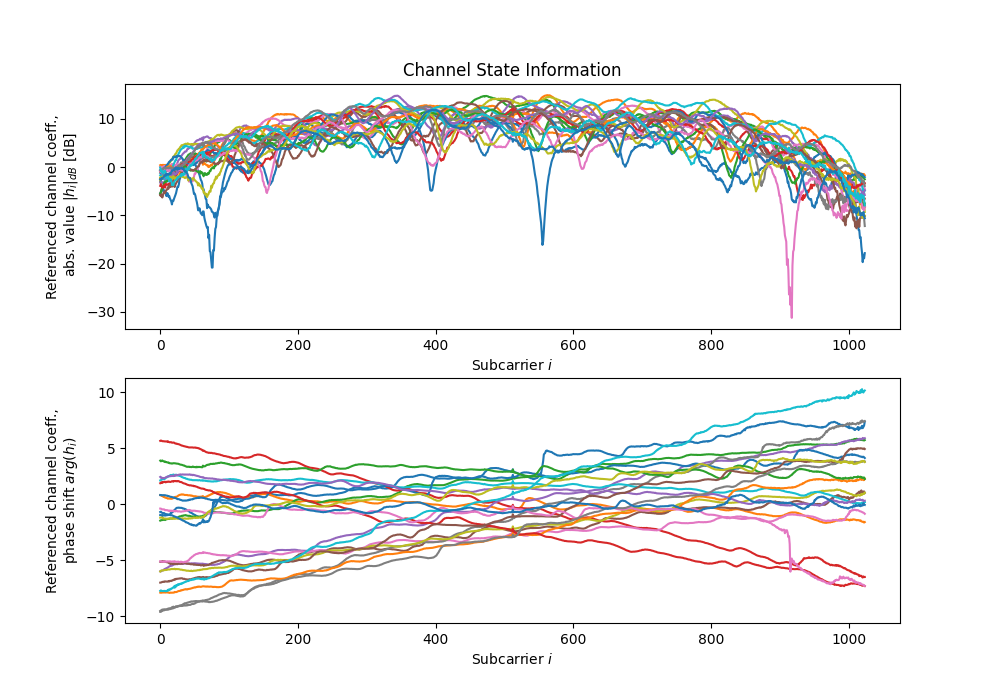
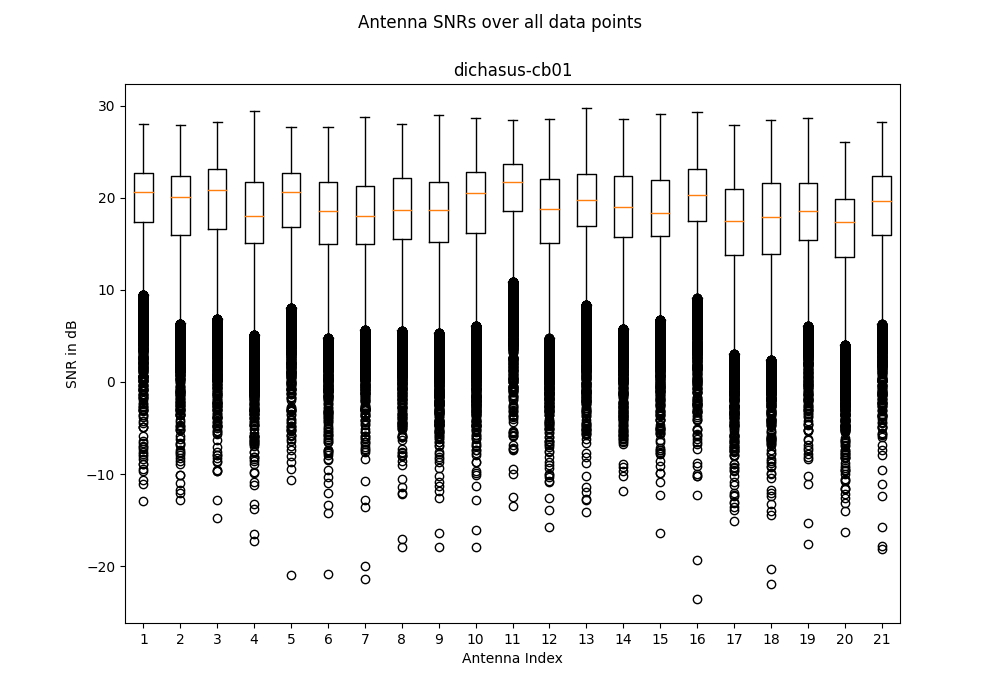
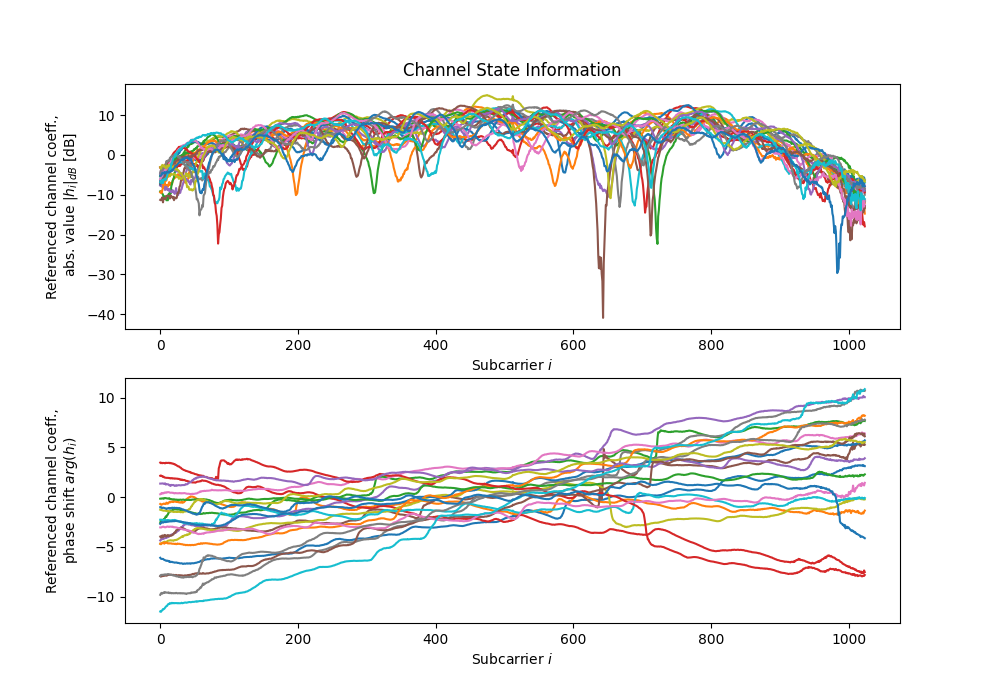
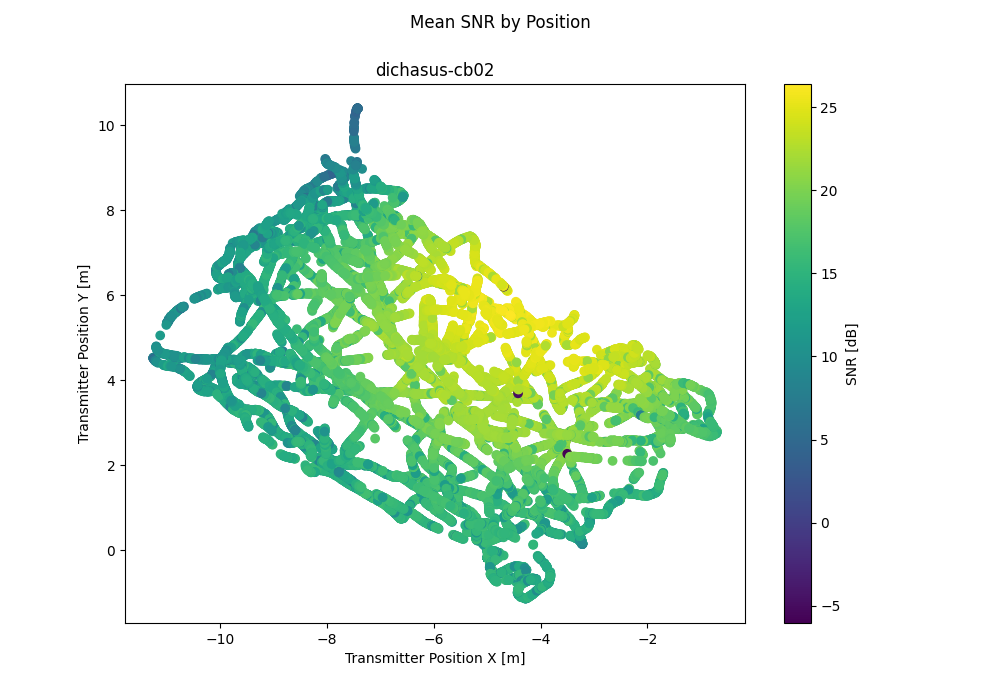
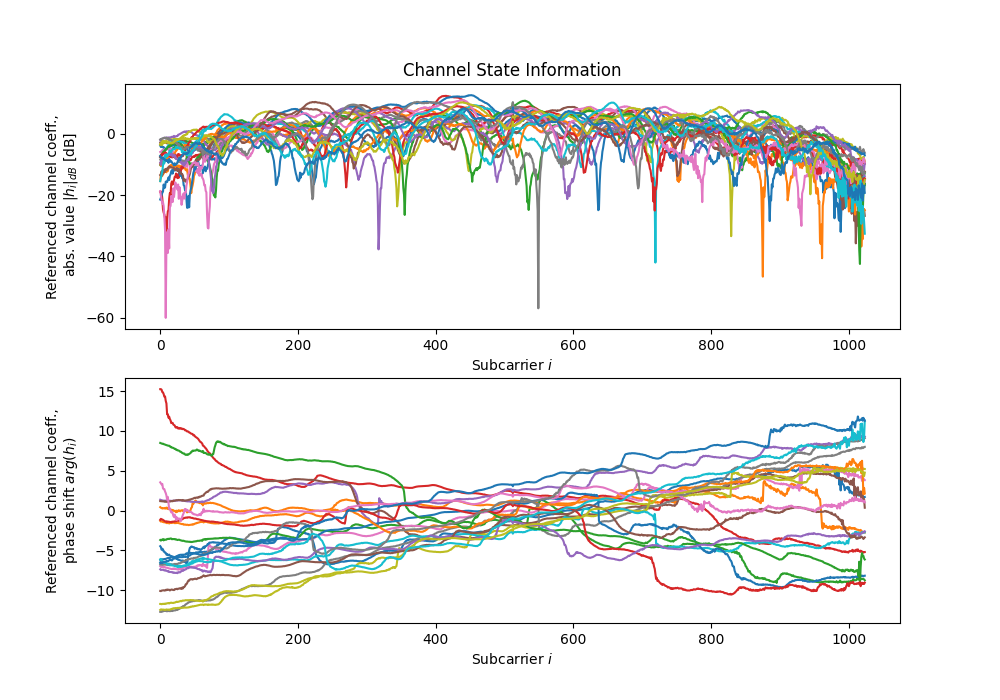
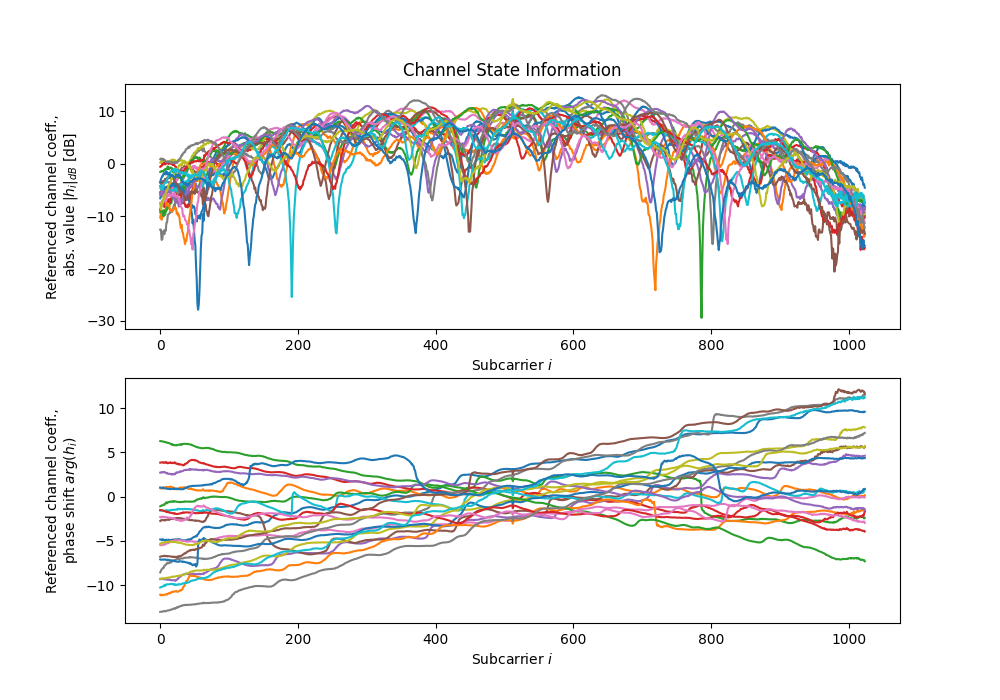
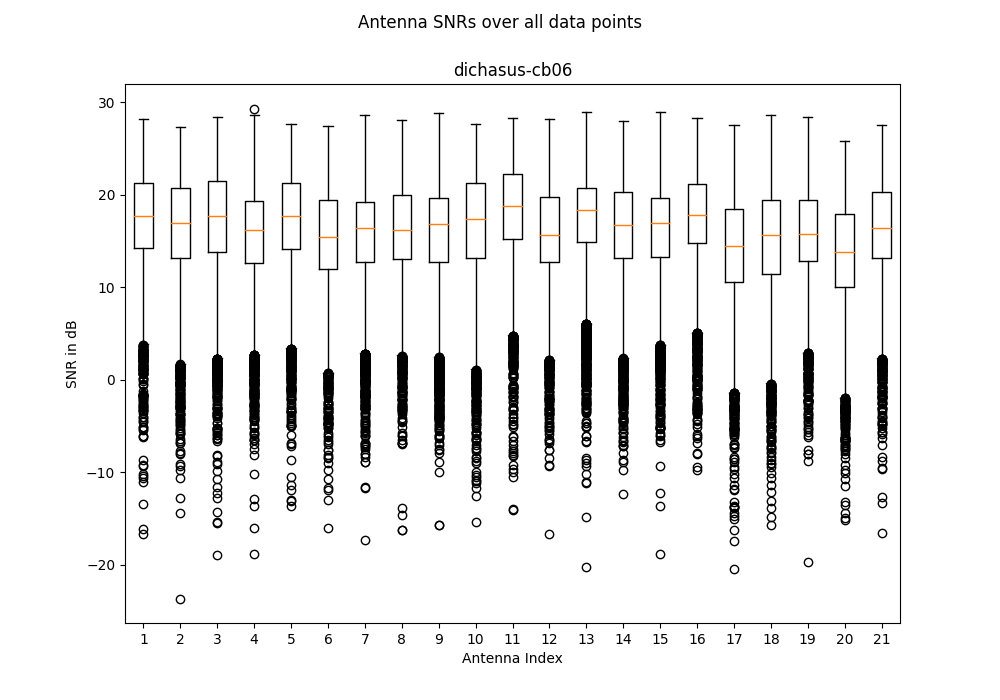
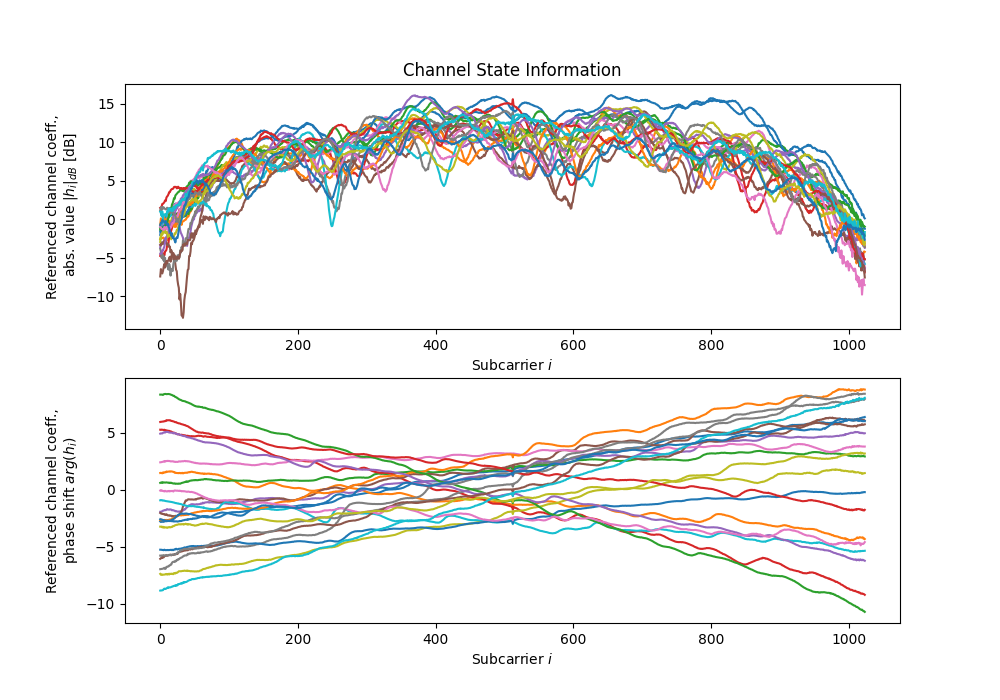
dichasus-cb0x Dataset: Industrial Environment LoS Day 2
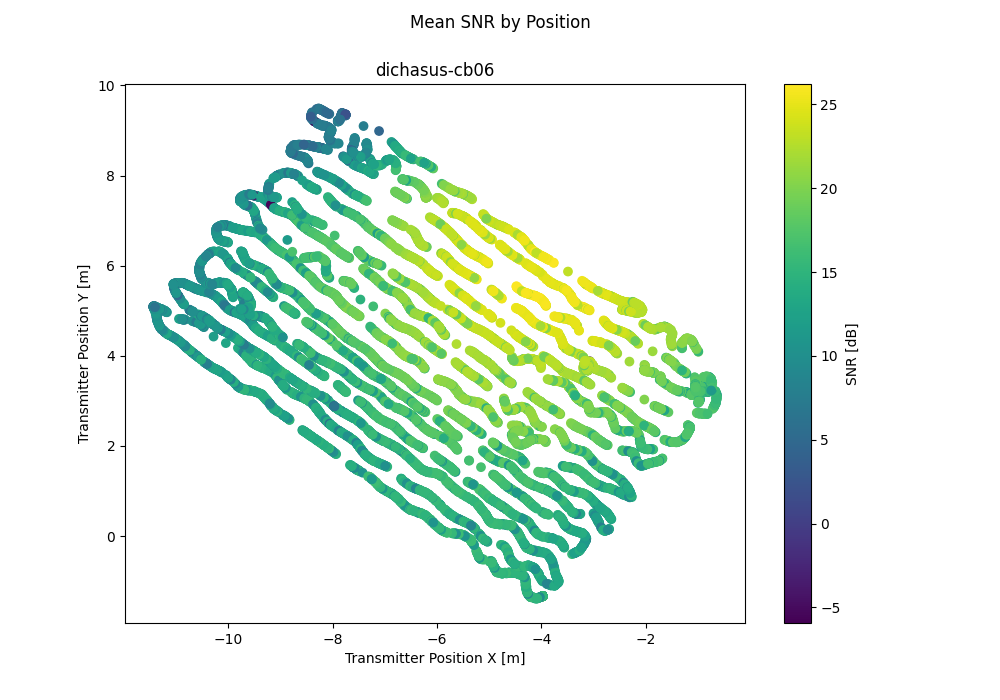
Line-of-Sight (LoS) area in the Arena2036 research factory campus environment.
Same as dichasus-ca0x, but measured on the second day with different reference transmitter channel and a different environment outside the measurement area (for example, a car body was moved to stand just outside of the measurement area).
50.000 MHz
Signal Bandwidth
1024
OFDM Subcarriers
140821
Data Points
7184.2 s
Total Duration
24.3 GB
Total Download Size
21
Number of Antennas
Indoor
Type of Environment
1.272000 GHz
Carrier Frequency
Co-Located
Antenna Setup
3D Tachymeter
Position-Tagged
Experiment Setup
The Arena 2036 factory floor. The measurement area is on the right at the very back of the hall. Source: ARENA2036 e.V.
Industiral equipment (e.g., forklifts, car bodies, machines, ...) was placed outside of the measurement area (unfortunately, we were not allowed to take pictures of everything).
The measurement was carried out in a corner of the Arena 2036 factory building.
A tachymeter was used to precisely track the position of the prism on top of the transmit antenna.
The robot with an ADALM-Pluto SDR as main transmitter and the antenna on top of a pole.
Data Analysis
Mean received signal-to-noise ratio by position
SNR by receive antenna index
Warnings
Due to a configuration error, we are unable to provide high-quality CSI data for all 32 antennas and at all locations. We had to disable certain antennas (as indicated below) and some transmitter locations are missing.
Antenna Configuration
Antenna 1: Main Array
This array has a vertical spacing of 0.118m and a
horizontal spacing of 0.118m.
In the dataset's cartesian coordinate system, its center is located at [-2.6706 7.878075 1.457425]
and the antenna points in direction [-0.86082768 -0.50889655 0].
Antenna Channel Assignments
| 0 | 10 | 19 | 2 | 4 | 1 | 9 | |
| 20 | 16 | 15 | 5 | ||||
| 18 | 7 | 11 | 13 | ||||
| 3 | 14 | 12 | 8 | 6 | 17 |
Python: Import with TensorFlow
#!/usr/bin/env python3
import tensorflow as tf
raw_dataset = tf.data.TFRecordDataset(["tfrecords/dichasus-cb00.tfrecords", "tfrecords/dichasus-cb01.tfrecords", "tfrecords/dichasus-cb02.tfrecords", "tfrecords/dichasus-cb03.tfrecords", "tfrecords/dichasus-cb04.tfrecords", "tfrecords/dichasus-cb05.tfrecords", "tfrecords/dichasus-cb06.tfrecords"])
feature_description = {
"csi": tf.io.FixedLenFeature([], tf.string, default_value = ''),
"gt-interp-age-tachy": tf.io.FixedLenFeature([], tf.float32, default_value = 0),
"pos-tachy": tf.io.FixedLenFeature([], tf.string, default_value = ''),
"snr": tf.io.FixedLenFeature([], tf.string, default_value = ''),
"time": tf.io.FixedLenFeature([], tf.float32, default_value = 0),
}
def record_parse_function(proto):
record = tf.io.parse_single_example(proto, feature_description)
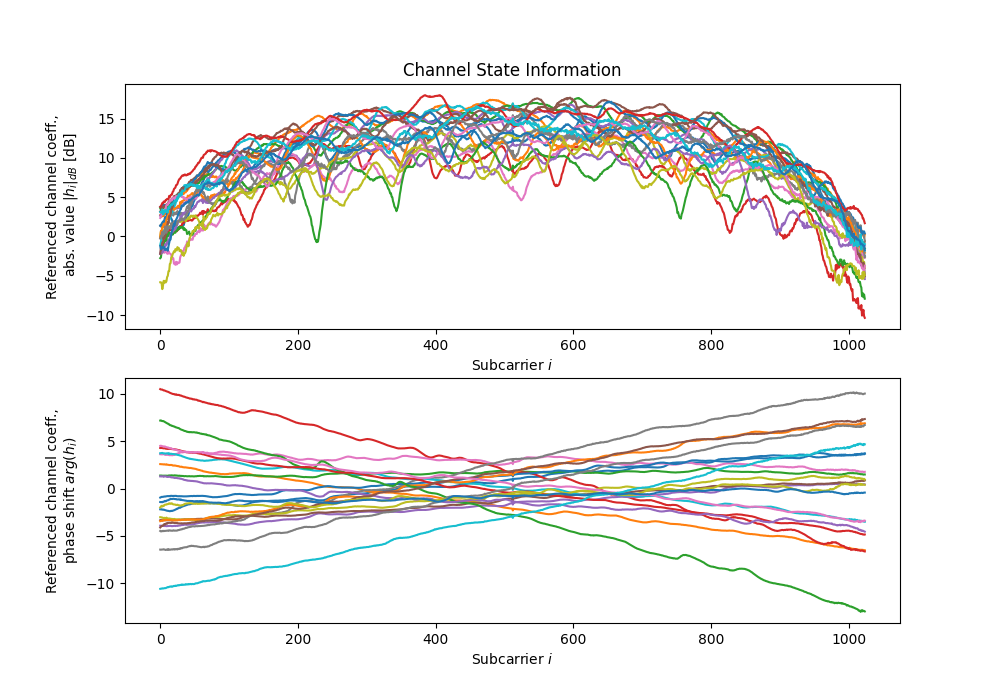
# Channel coefficients for all antennas, over all subcarriers, real and imaginary parts
csi = tf.ensure_shape(tf.io.parse_tensor(record["csi"], out_type = tf.float32), (21, 1024, 2))
# Time in seconds to closest known tachymeter position. Indicates quality of linear interpolation.
gt_interp_age_tachy = tf.ensure_shape(record["gt-interp-age-tachy"], ())
# Position of transmitter determined by a tachymeter pointed at a prism mounted on top of the antenna, in meters (X / Y / Z coordinates)
pos_tachy = tf.ensure_shape(tf.io.parse_tensor(record["pos-tachy"], out_type = tf.float64), (3))
# Signal-to-Noise ratio estimates for all antennas
snr = tf.ensure_shape(tf.io.parse_tensor(record["snr"], out_type = tf.float32), (21))
# Timestamp since start of measurement campaign, in seconds
time = tf.ensure_shape(record["time"], ())
return csi, gt_interp_age_tachy, pos_tachy, snr, time
dataset = raw_dataset.map(record_parse_function, num_parallel_calls = tf.data.experimental.AUTOTUNE)
# Optional: Cache dataset in RAM for faster training
dataset = dataset.cache()Reference Channel Compensation
For this dataset, we are able to provide estimated antenna-specific carrier phase and sampling time offsets. These offsets occur due to the fact that the reference transmitter channel is not perfectly frequency-flat. To learn more about why these offsets occur and about their compensation, visit our offset calibration tutorial on this topic. Note that the estimates provided here are "best-effort" calculations. The phase and time offsets between antennas in the same array are usually very accurate, but for antennas that are spaced far apart, the results may be less precise. For this dataset, the reference transmitter channel seems to be somewhat unstable, i.e., phase and time offsets fluctuate over time. Therefore, we provide a file containing our phase and time offset estimates for each individual file in the dataset. You can download these estimates from the list of files below.How to Cite
Please refer to the home page for information on how to cite any of our datasets in your research. For this dataset in particular, you may use the following BibTeX:
@data{dataset-dichasus-cb0x,
author = {Euchner, Florian and Gauger, Marc},
publisher = {DaRUS},
title = {{CSI Dataset dichasus-cb0x: Industrial Environment LoS Day 2}},
doi = {doi:10.18419/darus-2604},
url = {https://doi.org/doi:10.18419/darus-2604},
year = {2022}
}Download
This dataset consists of 7 files. Descriptions of these files as well as download links are provided below.
dichasus-cb00
dichasus-cb01
dichasus-cb02
dichasus-cb03
dichasus-cb04
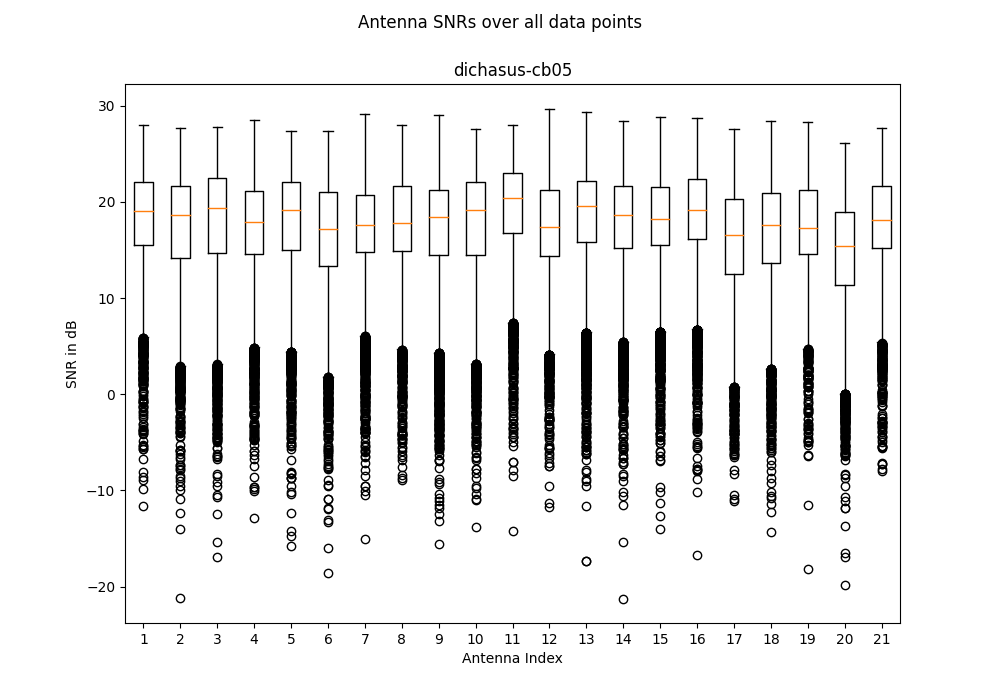
dichasus-cb05
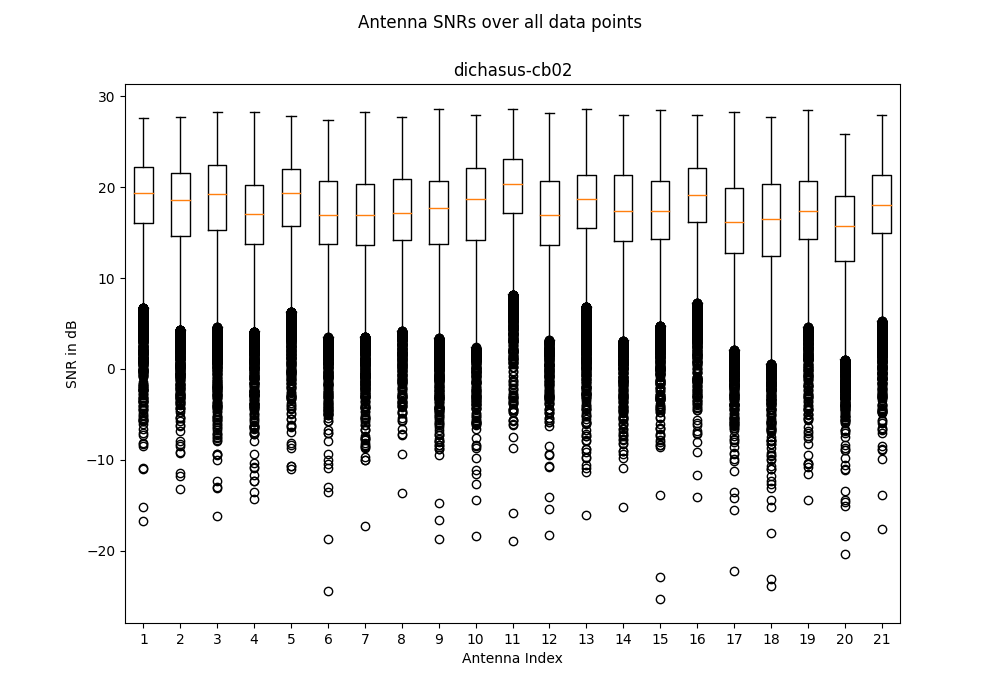
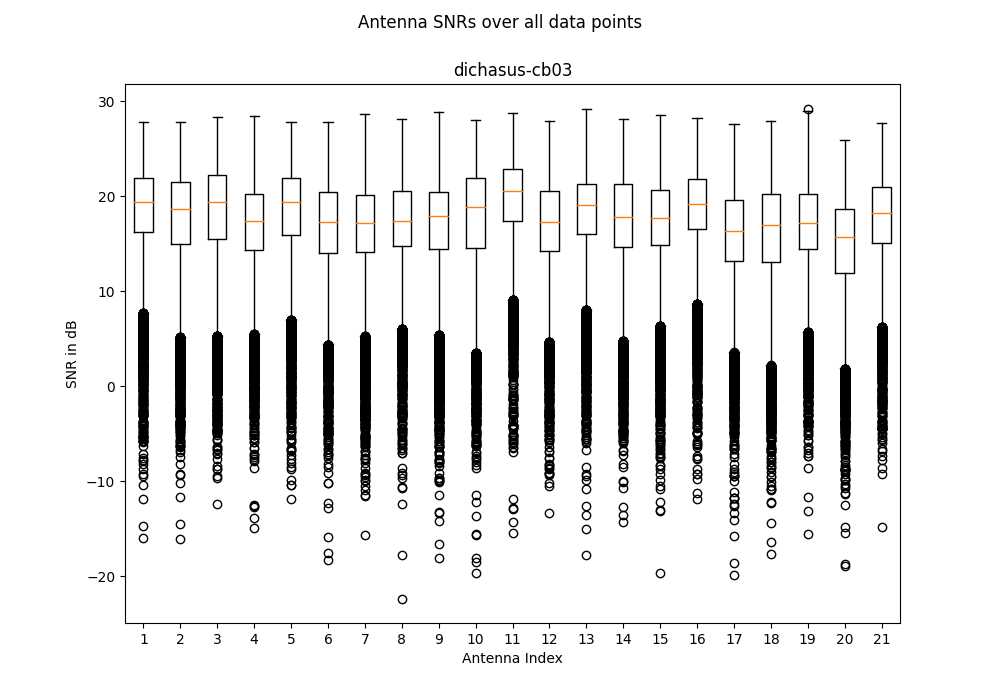
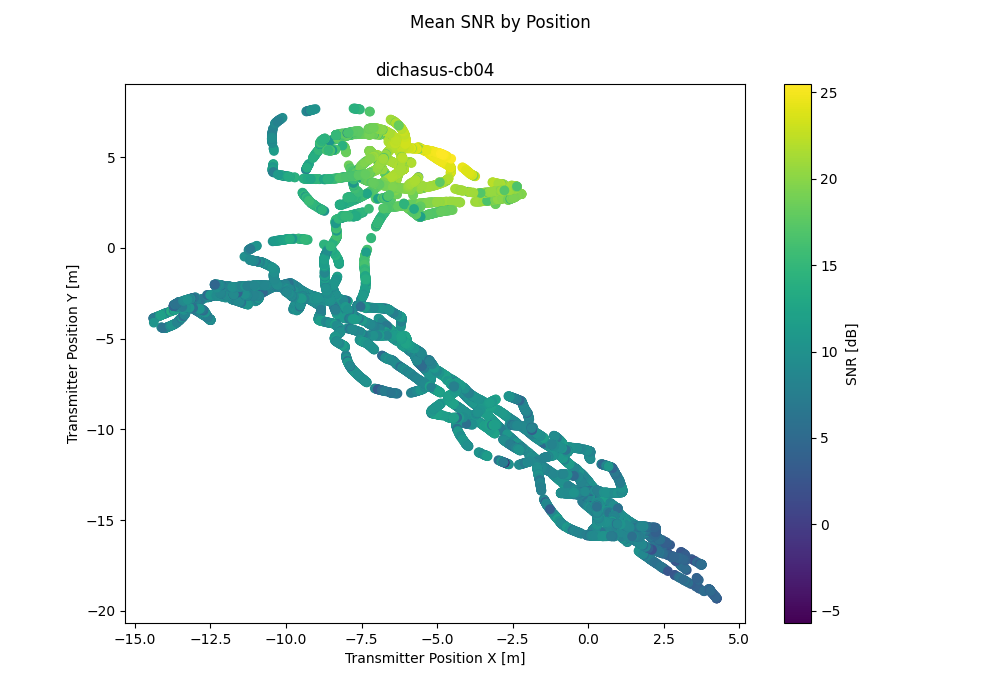
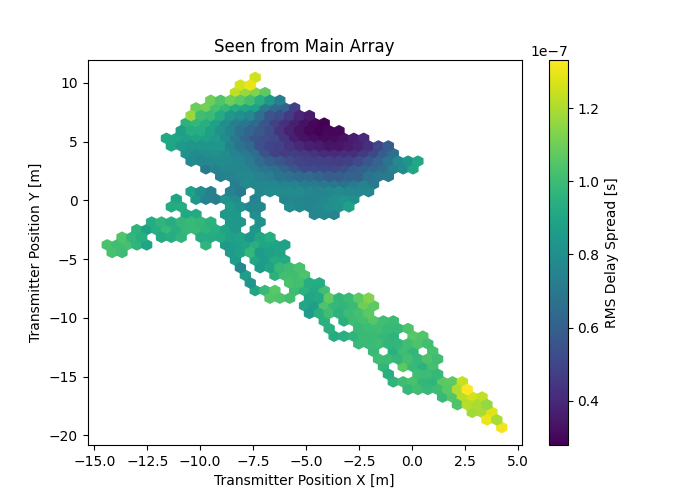
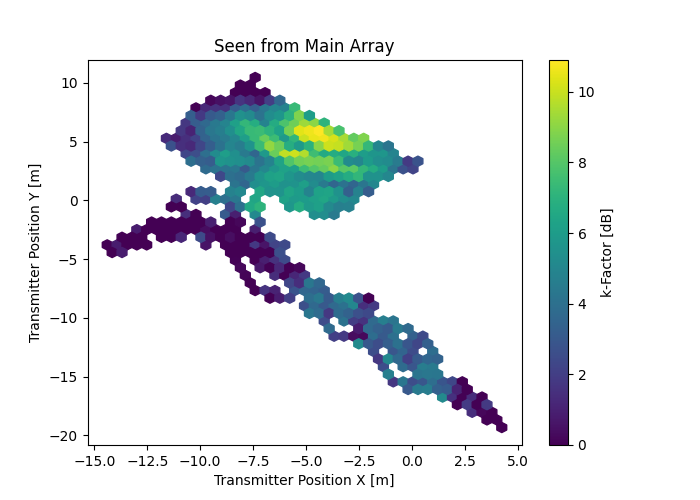
Derived Channel Statistics
Channel statistics such as delay spread, k-Factor and path loss exponent are a good way to characterize a wireless channel measurement and to parametrize a channel model. Using estimation algorithms contributed by Janina Sanzi, we automatically extract the following channel statistics from the measured datasets:
RMS Delay Spread
The delay spread of a wireless channel is inversely proportional to the channel's coherence bandwidth and indicates how "spread out" the lengths of the various multipath propagation paths are. For every datapoint, the delay spread can be characterized by its root mean square value and the resulting delay spreads can be plotted over the measurement area:
Rician K-Factor
The Rician K-factor is defined as the power ratio between dominant and diffuse component, usually expressed in decibels. We estimate the K-factor with a moment-method based on the distribution of of channel coefficient powers. The resulting K-Factors be plotted over the measurement area: